音を見てみよう - 名古屋作曲の会（旧：名大作曲同好会）

名作同理工系部門担当（自称）、sawapyです。前回の僕の記事、spleeterの紹介が好評だったため、今回も理工系の内容でいこうと思います。

今回は前置きも無しにいきなり・・・

音を見てみましょう！！！

「「「「は？？？？？？？？」」」」

ーそうです。仰る通り音は本来耳で聴くもの。ですが、今回はその音を見てみようという記事になっております。時にはアッと感動したり、時には頭が痛くなるような内容が出てくるかもしれませんが、最後までお付き合い頂ければ幸いです。

1.はじめに
2.波形
3.数学的なアプローチその1：sin波
4.数学的なアプローチその2：倍音とは
5.数学的なアプローチその3：フーリエ変換
6.まとめ
7.おまけ：オーディオビジュアライザー

1.はじめに

この記事を書こうと思ったきっかけは、とあるドラマーの友達の一言でした。

「同じ音を色んな楽器で色んな音色で出せるってすごいよな」

ちょっと詳しく見てみましょう。
「同じ音」とは、恐らく「同じ音高の音」という意味だったのでしょう。例えば、真ん中のド。リコーダーで吹いても、ピアノで弾いても、ギターで鳴らしても、同じ基本周波数262Hzを持つC4という音に変わりはありません。それが、リコーダーやピアノ、ギターといった様々な楽器で鳴らすことで多種多様な音色で彩られる。このことに彼は感動したのでしょう。

ではこの違いはどこから生まれるのでしょうか。

この問いに答えるには、音を数学的に解析することで、また、それをグラフとして描画することでわかりやすく説明できるのではないかと考え、この記事の執筆に至りました。

2.波形

この問いに対する最もシンプルでわかりやすい説明は、波形を見ることでしょう。下の画像は、それぞれバイオリンとピアノでA4（真ん中のドの右側のラの音、440Hz）を鳴らした時の波形を拡大したものです。

・バイオリン

f:id:nu-composers:20200125160614p:plain

・ピアノ

f:id:nu-composers:20200125160607p:plain

違いが一目瞭然ですよね。
周波数とは、周期的に変化するものが、1秒間に何回周期運動をするかという数字です。この場合、1秒間に440回、この波が繰り返されているわけですね。この事実はどの楽器A4の音を鳴らしても変わりませんが、その波一つ一つの形が違うため、音色が異なって聴こえていたのですね。

どうでしょうか、音を目で見ればわかりやすいのではないでしょうか。

3.数学的なアプローチその1：sin波

ところで、最もシンプルな音色ってなんだと思いますか？

様々な視点がありますが、ここでは最もシンプルな音色として純音、つまりsin波を取り上げたいと思います。コイツに高校の数学で苦しめられた記憶が蘇った方も多いかと思います。僕もその1人です。さて、sin関数といえば、こんな形ですよね。

f:id:nu-composers:20200125160611p:plain

うむ、美しい

滑らかなカーブの連続として描画されていますね。このsin波、実際に鳴らしてみるとこんなカンジ。

聴き覚えありませんか？
実は時報や音叉の音が、このsin波にかなり近い音だと言われています。ほとんどsin波そのものと言ってもいいかもしれません。

そしてなんと！！あらゆる音色は、このsin波を重ね合わせることによって作り出すことができるのです！！！

「は？？？？」という声が聞こえてきそうですが、数学がそれを裏付けています（詳しくは５章）。また、純音という名前からも、すべての元となりそうな感じが伝わってくるかもしれません。
逆に、上で挙げたような、いわゆる楽器から鳴る音は全てこのsin波の組み合わせでできているということです。

次章以降では、「倍音」というものに注目して、音色ができる仕組みを考えていこうと思います。

4.数学的なアプローチその2：倍音とは

「倍音とは、楽音の音高とされる周波数に対し、2以上の整数倍の周波数を持つ音の成分。」（Wikipediaより）
先程見ていただいた、バイオリンとピアノの波形は、sin波とはかけ離れたものだったかと思います。

それもそのはず。

ほとんどの音は、基本となる周波数の整数倍の周波数の音を含んでいます。つまり、バイオリンで440HzのA4を鳴らせば、同時に880Hz（A5）、1320Hz（E6）、1760Hz（A6）、2200Hz（C＃7）、・・・の音も同時に鳴っていることになります。ただしこれらの音が同じ音量で鳴っているわけではなく、強さが少しずつ異なり、また、グラフにした時の開始点（位相と呼びます）がズレています。この倍音の含み方の特性が楽器ごとに異なるため、楽器によって波形が異なり、様々な音色が生み出されるということになります。

では次章では、この倍音の含まれ方を解析してみたいと思います。

5.数学的なアプローチその3：フーリエ変換

注意！この章の内容は結構難しめです。グラフだけ追って、本文はサラッと読み飛ばすくらいがちょうどいいかもしれません。

さて物騒な前置きから始まりましたが、倍音を詳しく解析していきましょう。
ここで登場するのは、理系大学生、特に工学系でお世話になるフーリエ変換というもの。詳しい説明は数学書に任せますが、コイツは時間領域を周波数領域に変換してくれます。つまり、2章や3章で示した音の信号は横軸が時間になっていますが、このデータをフーリエ変換（この場合はデジタル信号なので、正確には離散フーリエ変換）してやると、横軸が周波数になります。
つまり、どの周波数がどれだけの強さで（複素数の位相も含めれば、どれだけの位相で）含まれているのか知ることができます。

では実際に変換してみましょう。

時間領域xに対する周波数領域Xを求めるフーリエ変換の式がこちら

$X (Ω) = \int_{- \infty}^{\infty} x (ω) ⅇ^{- i ω t} d t$

「「「「は？？？？」」」」

やっていることは、元の信号に複素指数関数をかけて無限範囲の時間で積分しているだけなのですが、初めて見ると頭が痛くなるような式ですね。まあ…コイツを人力で積分するのはそこそこしんどいです。

・・・そんなわけで

実際にプログラムを書いて、どの周波数が含まれているのかコンピュータに分析させてみました。なお、使用言語はPythonで、numpyなどのライブラリを使用しています。

#必要なライブラリの読み込み
import numpy as np
import librosa
import matplotlib.pyplot as plt

def show_freq(filename,sampling_rate=44100):
    #オーディオファイルの読み込み
    wav, _ = librosa.load(filename, sr=sampling_rate)
    #高速フーリエ変換(離散フーリエ変換の一種)
    fft = np.fft.fft(wav*np.hanning(len(wav)))
    #周波数の強度のみを取り出すため絶対値をとる 見やすくするために表示する領域を限定
    abs = np.abs(fft[0:len(fft)//16])/1000

    #グラフの出力
    plt.plot(abs)
    plt.title(filename)
    plt.xlabel("frequency")
    plt.ylabel("amplitude")
    plt.tight_layout()
    plt.show()

show_freq("vln.wav")
show_freq("pf.wav")
show_freq("sin.wav")

読み込んだオーディオファイルの名前は、それぞれvln.wav、pf.wav、sin.wavです。

それでは、出力されたグラフを見てみましょう。

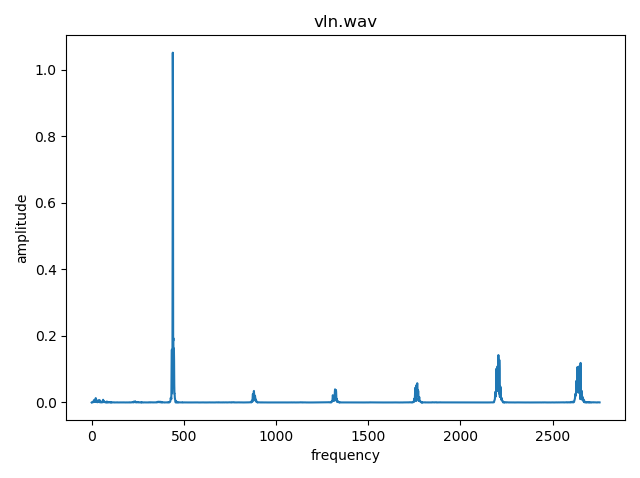
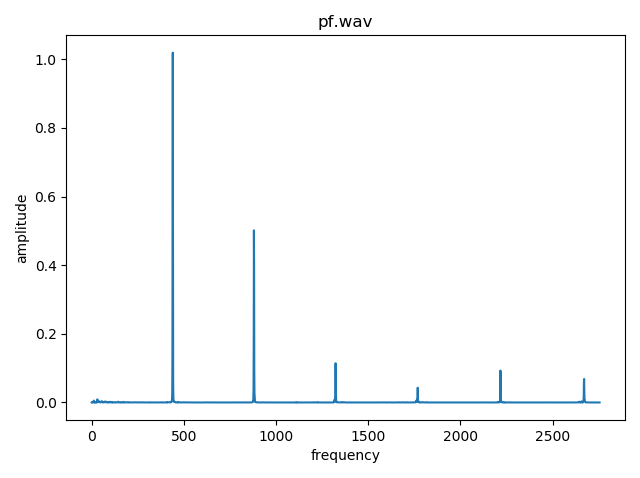
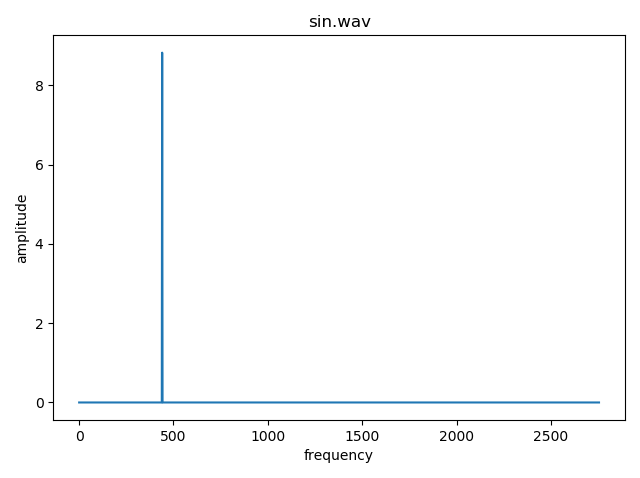
左から順にバイオリン、ピアノ、sin波です。

sin波には440Hzの成分しか含まれておらず、バイオリン、ピアノには４４０の整数倍の周波数をもった成分も含まれていることがわかりますね。

今回は、ソフトウェア音源という機械的に作られた音をそのまま使用しているため、とても綺麗に整数倍の部分だけに信号が立っています。（生楽器がどうなるのか気になった方は、「楽器　スペクトログラム」などで検索すると出てきます。実行環境がある方は、上のソースコードをファイル名を改変して実行してもいいですね。）

逆に、グラフの通りの強さのsin波を重ねれば（正確には、今回は説明を省略した位相の情報も必要ですが）バイオリンやピアノ、あらゆる楽器の音を作れてしまいます。

それを数学的に計算するものが、フーリエ逆変換というもので、sin波の各周波数成分の強さを与えると音のデータを返してくれます。（詳細は割愛）

周波数のパターンだけ音色が生まれる。

そのパターンは無限大。

つまりsin波だけであらゆる音色が作れる。

これが、３章の「sin波であらゆる音を作れる」と言った理由です。